We are given the head node root of a binary tree, where additionally every node’s value is either a 0 or a 1.
Return the same tree where every subtree (of the given tree) not containing a 1 has been removed.
(Recall that the subtree of a node X is X, plus every node that is a descendant of X.)
Example 1: Input: [1,null,0,0,1] Output: [1,null,0,null,1] Explanation: Only the red nodes satisfy the property "every subtree not containing a 1". The diagram on the right represents the answer.
Example 2: Input: [1,0,1,0,0,0,1] Output: [1,null,1,null,1]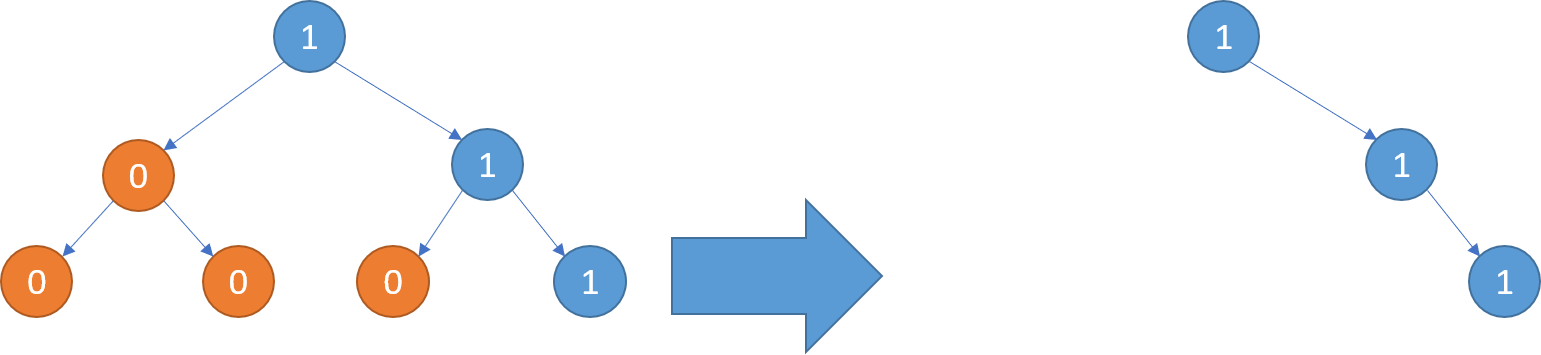
Example 3: Input: [1,1,0,1,1,0,1,0] Output: [1,1,0,1,1,null,1]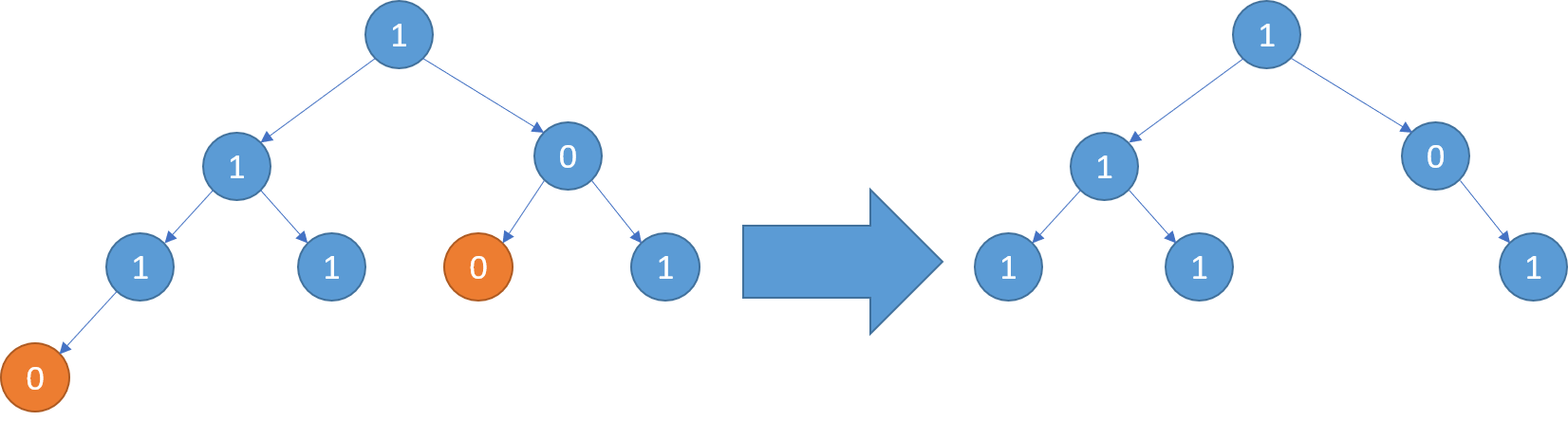
Note:
- The binary tree will have at most
200 nodes. - The value of each node will only be
0or1.
Solution: (Recursion)
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var pruneTree = function(root) {
// basic case:
if (root === null) return root;
root.left = pruneTree(root.left);
root.right = pruneTree(root.right);
// found 1 or has children then no need to remove
if (root.val === 1 || root.left || root.right)
return root;
else // remove node
return null;
};