Press "Enter" to skip to content

Posts tagged as “Tree”

LeetCode 297. Serialize and Deserialize Binary Tree (javascript)

By stone on April 21, 2021

Serialization is the process of converting a data structure or object into a sequence of bits so that it can be stored in a file or memory buffer, or transmitted across a network connection link to be reconstructed later in the same or another computer environment.

Design an algorithm to serialize and deserialize a binary tree. There is no restriction on how your serialization/deserialization algorithm should work. You just need to ensure that a binary tree can be serialized to a string and this string can be deserialized to the original tree structure.

Clarification: The input/output format is the same as how LeetCode serializes a binary tree. You do not necessarily need to follow this format, so please be creative and come up with different approaches yourself.

Example 1:

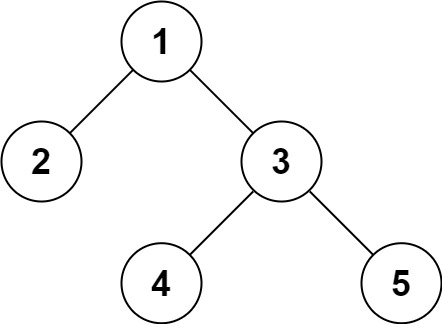
Input: root = [1,2,3,null,null,4,5]
Output: [1,2,3,null,null,4,5]

Example 2:

Input: root = []
Output: []

Example 3:

Input: root = [1]
Output: [1]

Example 4:

Input: root = [1,2]
Output: [1,2]

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • -1000 <= Node.val <= 1000

Idea: (Recursion)

We can encodes the tree to a single string.
// # indicates reach to the leave
Convert above tree to 12##34##56##

Time Complexity O(n)

Solution:

/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */

/**
 * Encodes a tree to a single string.
 *
 * @param {TreeNode} root
 * @return {string}
 */
var serialize = function(root) {
    let res = [];
    serializer(root, res);
    return res.join(",");
};

var serializer = function(root, output) {
    if (root === null) {
        output.push("#");
        return;
    }
    output.push(root.val);
    serializer(root.left, output);
    serializer(root.right, output);
}

// Decodes your encoded data to tree.
var deserialize = function(data) {
    data = data.split(",");
    let index = 0;
    
    function deserializer(data) {
        if(index > data.length || data[index] === "#") {
            return null;
        }
        let root = new TreeNode(parseInt(data[index]));
        index++;
        root.left = deserializer(data);
        index++;
        root.right = deserializer(data);
        return root;
    }
    return deserializer(data);
};

LeetCode 129. Sum Root to Leaf Numbers (javascript)

By stone on April 13, 2021

You are given the root of a binary tree containing digits from 0 to 9 only.

Each root-to-leaf path in the tree represents a number.

  • For example, the root-to-leaf path 1 -> 2 -> 3 represents the number 123.

Return the total sum of all root-to-leaf numbers.

A leaf node is a node with no children.

Example 1:

Input: root = [1,2,3]
Output: 25
Explanation:
The root-to-leaf path 1->2 represents the number 12.
The root-to-leaf path 1->3 represents the number 13.
Therefore, sum = 12 + 13 = 25.

Example 2:

Input: root = [4,9,0,5,1]
Output: 1026
Explanation:
The root-to-leaf path 4->9->5 represents the number 495.
The root-to-leaf path 4->9->1 represents the number 491.
The root-to-leaf path 4->0 represents the number 40.
Therefore, sum = 495 + 491 + 40 = 1026.

Constraints:

  • The number of nodes in the tree is in the range [1, 1000].
  • 0 <= Node.val <= 9
  • The depth of the tree will not exceed 10.

Idea:

Use DFS Template

Solution 1:

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var sumNumbers = function(root) {
    if (root === null) return;
    let res = [];
    let cur = [];
    dfs(root, res, cur);
    let sum = 0;
    for (let num of res) {
        sum += num;
    }
    return sum;
};

function dfs(root, res, cur) {
    // exit recursion:
    if (root === null) return;
    // found leaf, save the number
    if (root.left === null && root.right === null) {
        cur.push(root.val);
        res.push(parseInt(cur.join('')));
        cur.pop();
        return;
    }
    
    // possible solution
    if (root !== null) {
        cur.push(root.val);
        dfs(root.left, res, cur);
        dfs(root.right, res, cur);
        cur.pop();
    }
    return;
}

Solution 2: (Version 2)

var sumNumbers = function(root) {
    if (root === null) return;
    let res = [0];
    let cur = [0];
    dfs(root, res, cur);
    return res[0];
};

function dfs(root, res, cur) {
    // exit recursion:
    if (root === null) return;
    // found leaf, save the number
    if (root.left === null && root.right === null) {
        cur[0] = cur[0] * 10 + root.val;
        res[0] += cur[0];
        cur[0] = (cur[0] - root.val) / 10;
        return;
    }
    
    // possible solution
    if (root !== null) {
        cur[0] = cur[0] * 10 + root.val;
        dfs(root.left, res, cur);
        dfs(root.right, res, cur);
        cur[0] = (cur[0] - root.val) / 10;
    }
    return;
}

LeetCode 112. Path Sum (javascript)

By stone on April 11, 2021

Given the root of a binary tree and an integer targetSum, return true if the tree has a root-to-leaf path such that adding up all the values along the path equals targetSum.

A leaf is a node with no children.

Example 1:

Input: root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22
Output: true

Example 2:

Input: root = [1,2,3], targetSum = 5
Output: false

Example 3:

Input: root = [1,2], targetSum = 0
Output: false

Constraints:

  • The number of nodes in the tree is in the range [0, 5000].
  • -1000 <= Node.val <= 1000
  • -1000 <= targetSum <= 1000

Solution: (Recursion)

  • Time complexity: O(n)
  • Space complexity: O(n)
/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {boolean}
 */
var hasPathSum = function(root, targetSum) {
    if (root === null) return false;
    if (root.val === targetSum && root.left === null && root.right === null) return true;
    return hasPathSum(root.left, targetSum - root.val) ||
           hasPathSum(root.right, targetSum - root.val);
};

LeetCode 814. Binary Tree Pruning (javascript)

By stone on April 9, 2021

We are given the head node root of a binary tree, where additionally every node’s value is either a 0 or a 1.

Return the same tree where every subtree (of the given tree) not containing a 1 has been removed.

(Recall that the subtree of a node X is X, plus every node that is a descendant of X.)

Example 1:
Input: [1,null,0,0,1]
Output: [1,null,0,null,1]
 
Explanation: 
Only the red nodes satisfy the property "every subtree not containing a 1".
The diagram on the right represents the answer.



Example 2:
Input: [1,0,1,0,0,0,1]
Output: [1,null,1,null,1]




Example 3:
Input: [1,1,0,1,1,0,1,0]
Output: [1,1,0,1,1,null,1]

Note:

  • The binary tree will have at most 200 nodes.
  • The value of each node will only be 0 or 1.

Solution: (Recursion)

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {TreeNode}
 */
var pruneTree = function(root) {
    // basic case:
    if (root === null) return root;
    root.left = pruneTree(root.left);
    root.right = pruneTree(root.right);
    // found 1 or has children then no need to remove
    if (root.val === 1 || root.left || root.right) 
        return root;
    else // remove node
        return null;
};