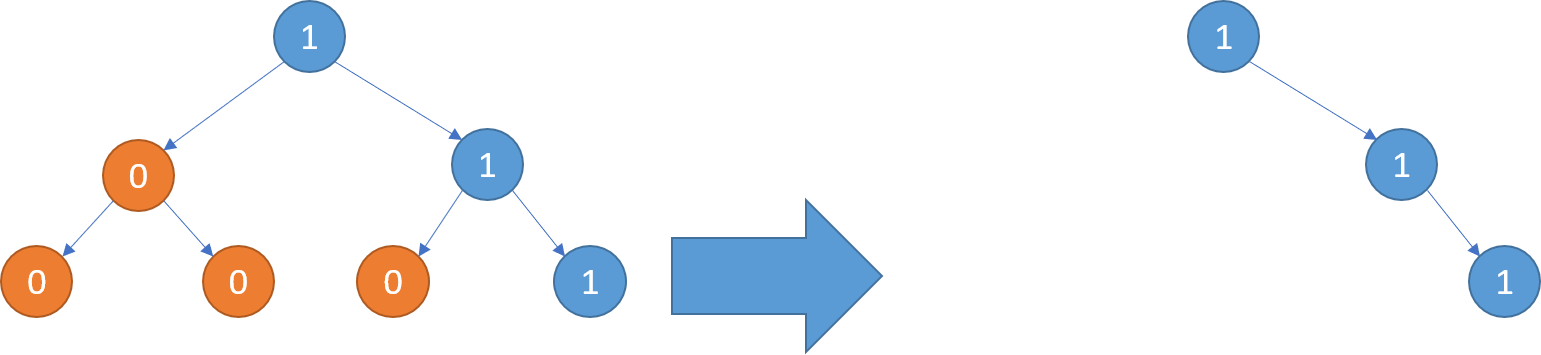
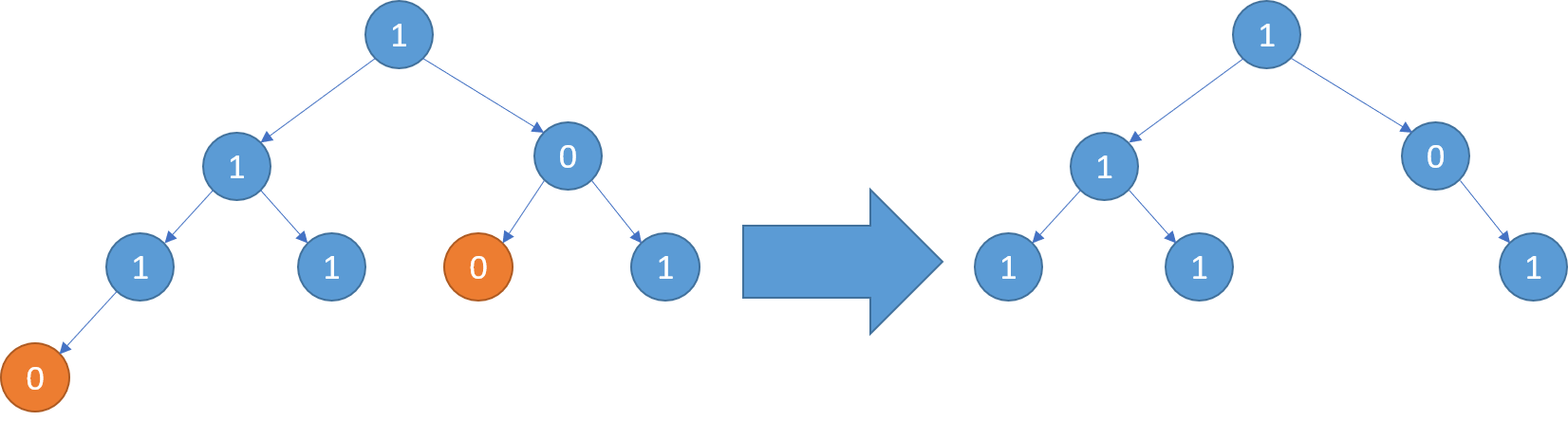
You are given the root of a binary search tree (BST) and an integer val.
Find the node in the BST that the node’s value equals val and return the subtree rooted with that node. If such a node does not exist, return null.
Example 1:
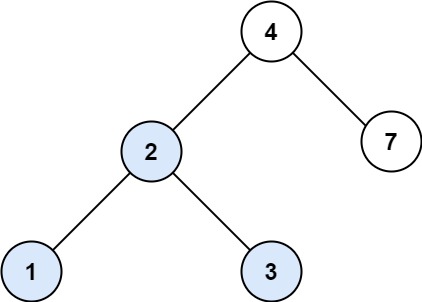
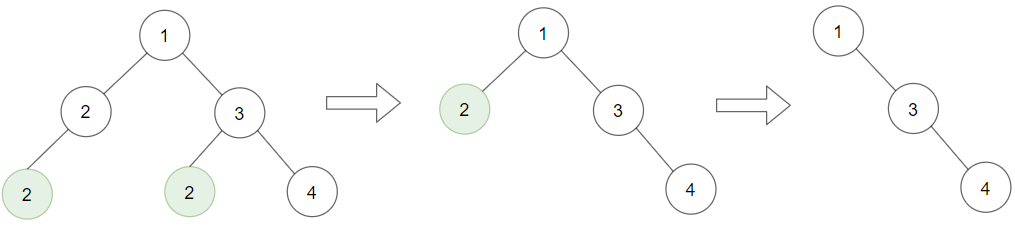
Input: root = [4,2,7,1,3], val = 2 Output: [2,1,3]
Example 2:
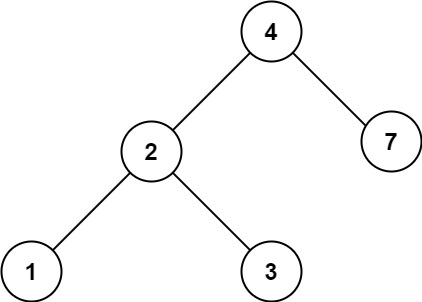
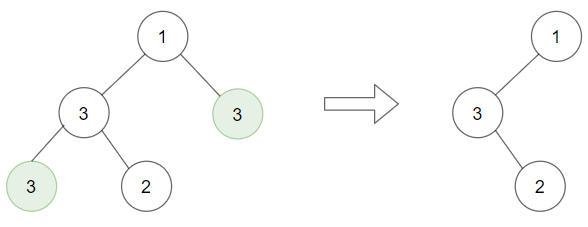
Input: root = [4,2,7,1,3], val = 5 Output: []
Constraints:
- The number of nodes in the tree is in the range
[1, 5000]. 1 <= Node.val <= 107rootis a binary search tree.1 <= val <= 107
Solution:
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
* @param {number} val
* @return {TreeNode}
*/
var searchBST = function(root, val) {
if (root === null) return null
if (root.val === val)
return root;
else if (val < root.val)
return searchBST(root.left, val);
else
return searchBST(root.right, val);
};