LeetCode 99. Recover Binary Search Tree (javascript)

You are given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Recover the tree without changing its structure.

Follow up: A solution using O(n) space is pretty straight forward. Could you devise a constant space solution?

Example 1:

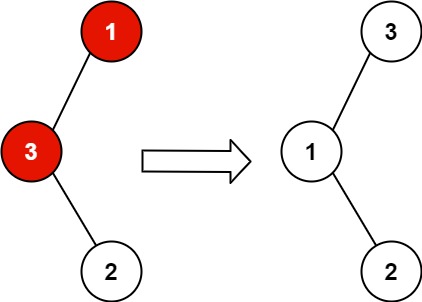
Input: root = [1,3,null,null,2]
Output: [3,1,null,null,2]
Explanation: 3 cannot be a left child of 1 because 3 > 1. Swapping 1 and 3 makes the BST valid.

Example 2:

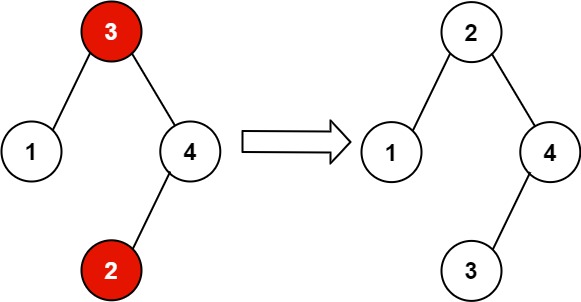
Input: root = [3,1,4,null,null,2]
Output: [2,1,4,null,null,3]
Explanation: 2 cannot be in the right subtree of 3 because 2 < 3. Swapping 2 and 3 makes the BST valid.

Constraints:

The number of nodes in the tree is in the range [2, 1000].
-2³¹ <= Node.val <= 2³¹ - 1

Idea:

Because inorder traverse BST, all values are sorted. We can use inorder traversal to find two nodes that have prev.val > root. val and swap them

Time complexity: O(n)
Space complexity: O(height)

Solution:

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var recoverTree = function(root) {
    // javascript can't pass value by reference 
    // so pass array object by reference
    let first = [null];
    let second = [null];
    let prev = [null];
    inorder(root, first, second, prev);
    [first[0].val, second[0].val] = [second[0].val, first[0].val];
};

function inorder(root, first, second, prev) {
    // Because inorder traverse BST, all values are sorted.
    // Using inorder traversal to find two nodes that have prev.val > root.val
    if (root === null) return;
    inorder(root.left, first, second, prev);
    if (prev[0] && prev[0].val > root.val) {
        if (first[0] === null) first[0] = prev[0];
        second[0] = root;
    }
    prev[0] = root;
    inorder(root.right, first, second, prev);
}