Posts published in “Algorithm Template”

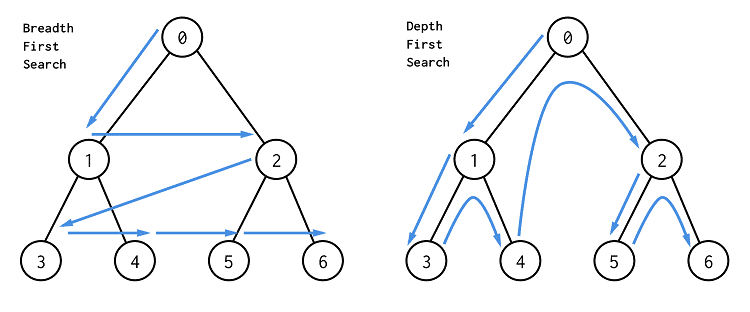
DFS Template

Use on Binary Tree, Permutation or Combination problems

• Time complexity：
  • Tree traversal: O(n)
  • Permutation: O(n! * n)
  • Combination: O(2ⁿ * n)

function dfs(nums, n, start, cur, res...) {
    if (exit recursive condition) {
        // record answer
        return;
    }
    for (possible solution) {
        // modify current state
        dfs(nums, n, i + 1, cur, res...);
        // recover current state

    }
    return something if need // option
};

BFS Template

Use on Topological Sorting, Level Traversal, Shortest path in graph, Union Find problems

• Time complexity：O(n + m) // n is node, m is edge
• Space complexity: O(n)

// 1. No level:
function bfs(node) {
    const queue = [];
    queue.push(node);
    
    while(queue.length !== 0) {
        ...
        let cur = queue.shift();
        for (neighbor in cur\'s neighbors) {
             if (neighbor is valid but not visit)
                queue.push(neighbor)
        }
    }
}
             
// 2. Has level traversal: depends on the questions
// Level could be a number or array
function bfs(node) {
    const queue = [];
    queue.push(node);
    // (1) let level = 0; // level as a number for tracking
    while(queue.length !== 0) {
        let size = queue.length;
        // (2) let level = []; // level could be storing data
        while(size--) {
            let cur = queue.shift();
            for (neighbor in cur\'s neighbors) {
                 if (neighbor is valid but not visit)
                    queue.push(neighbor)
            }
        }
        //(1) level++;
        //(2) res.push(level.concat()); // adding to the result
    }
}
                 
// 3. BFS - finding the shortest path in graph
function bfs(node) {
    const queue = [];
    let distance = new Map(); // avoid duplicate, track startNode
    queue.push(startNode);
    distance.set(startNode, 0); // or 1 depends on the question
    
    while(queue.length !== 0) {
        let cur = queue.shift();
        if (node is destination) {
            break or return something;
        }
        for (neighbor in cur\'s neighbors) {
             if (distance.has(neighbor)) continue;
             queue.push(neighbor);
             distance.set(neighbor, distance.get(node) + 1);
        }
    }
    // possible return:
    return distance;
    return distance.keys();
    return distnace.get(endNode);
    ...
}

Topological Sorting (BFS) Template:

function topologicalSort(nodes) {
    const queue = [];
    let indegrees = getIndegrees(nodes); // 统计所有点的入度信息 as hashmap
    // add those indegree === 0 nodes into queue
    for (node of nodes) {
        if (indegrees.get(node) === 0)
            queue.push(node);
    }
    
    let topoOrder = [];
    while(queue.length !== 0) {
        let cur = queue.shift();
        topoOrder.push(cur);
        for (neighbor in cur\'s neighbors) {
             indegrees.set(neighbor, indegrees.get(neighbor) - 1);
             // when indegree is 0, no more depends on any node, add to queue
             if (indegrees.get(neighbor) === 0) {
                queue.push(neighbor);
        }
    }
    if (topoOrder.length !== nodes.length)
        return "No topoOrder!";
    
    return topoOrder;
}

Binary Search Template

• Time complexity O(logn)
• Space complexity O(1)

function binarySearch(nums, target) {
    let l = 0;
    let r = nums.length;
    
    while (l < r) {
        let mid = l + Math.floor((r - l) / 2);
        if (nums[mid] === target) {
            // most case: just return target
            return mid;
            // --- if searching leftBound
            // leftBound = mid;
            // r = mid;
            // --- if searching rightBound
            // rightBound = mid;
            // l = mid + 1;
        } else if (nums[mid] > target) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
}

Merge Sort Template

var sortArray = function(nums) {
    if (nums === null || nums.length === 0) return;
    let temp = [];
    mergeSort(nums, 0, nums.length - 1, temp);
    return nums;
};

function mergeSort(nums, start, end, temp) {
    if (start >= end) return;
    // deal with first half
    mergeSort(nums, start, Math.floor((start + end) / 2), temp);
    // deal with second half
    mergeSort(nums, Math.floor((start +end) / 2) + 1, end, temp);
    // merge
    merge(nums, start, end, temp);
}

function merge(nums, start, end, temp) {
    let mid = Math.floor((start + end) / 2);
    let l_index = start;
    let r_index = mid + 1;
    let index = start;
    while (l_index <= mid && r_index <= end) {
        if (nums[l_index] < nums[r_index]) {
            temp[index++] = nums[l_index++];
        } else {
            temp[index++] = nums[r_index++];
        }
    }
    while (l_index <= mid)
        temp[index++] = nums[l_index++];
    while (r_index <= end)
        temp[index++] = nums[r_index++];
    for (let i = start; i <= end; i++) {
        nums[i] = temp[i];
    }
}

Quick Sort Template

var sortArray = function(nums) {
    if (nums === null || nums.length === 0) return;
    quickSort(nums, 0, nums.length - 1)
    return nums;
};

function quickSort(nums, left, right) {
    let index;
    if (nums.length > 1) {
        // index returned from partition
        index = partition(nums, left, right);
        // more elements on the left side of the pivot
        if (left < index - 1)
            quickSort(nums, left, index - 1);
        // more elements on the right side of the pivot
        if (index < right)
            quickSort(nums, index, right);
    }
    // you can return or not return, 
    // since we change nums, no need to return
    // return nums;
}

function partition(nums, start, end) {
    let l = start, r = end;
    let mid = Math.floor((start + end) / 2);
    let pivot = nums[mid];
    // Important: l <= r not l < r
    while (l <= r) {
        while(nums[l] < pivot)
            l++;
        while(nums[r] > pivot)
            r--;
        if (l <= r) {
            // swap
            [nums[l], nums[r]] = [nums[r], nums[l]];
            l++;
            r--;
        }
    }
    return l;
}

To be continue…