LeetCode 74. Search a 2D Matrix (javascript)

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

Integers in each row are sorted from left to right.
The first integer of each row is greater than the last integer of the previous row.

Example 1:

Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
Output: true

Example 2:

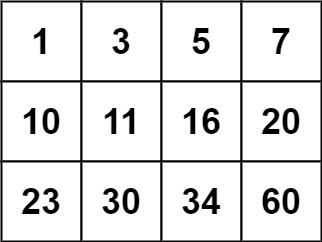
Input: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
Output: false

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-10⁴ <= matrix[i][j], target <= 10⁴

Solution 1: (DFS)

/**
 * @param {number[][]} matrix
 * @param {number} target
 * @return {boolean}
 */
var searchMatrix = function(matrix, target) {
    return dfs(matrix, target, 0, 0);
};

function dfs(matrix, target, x, y) {
    let rows = matrix.length;
    let cols = matrix[0].length;
    
    // exit recursion condition, reach to the end;
    if (y === rows) return false;
    
    // traverse from left to right, then next row
    let nextX = (x + 1) % cols;
    let nextY = nextX === 0 ? y + 1 : y;

    // found return true or not found, DFS next element
    if (matrix[y][x] === target) 
        return true;
    else
        return dfs(matrix, target, nextX, nextY);

    return false;
}

Solution 2: (Binary Search) Better and Faster!

Time complexity: O(log(mn))
Space complexity: O(1)

var searchMatrix = function(matrix, target) {
    let cols = matrix[0].length;
    // 	treat 2D as 1D, use binary search
    let l = 0;
    let r = matrix.length * cols;
    while (l < r) {
        let mid = l + Math.floor((r - l) / 2);
        let row = Math.floor(mid / cols);
        let col = mid % cols;
        if (matrix[row][col] === target) {
            return true;
        } else if (matrix[row][col] > target) {
            r = mid;
        } else {
            l = mid + 1;
        }
    }
    return false;
};