LeetCode 64. Minimum Path Sum (javascript)

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right, which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

Example 1: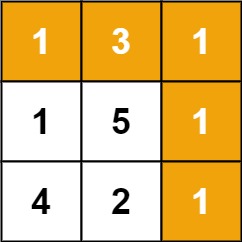

Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.

Example 2:

Input: grid = [[1,2,3],[4,5,6]]
Output: 12

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 200
• 0 <= grid[i][j] <= 100

Idea:

Dynamic Programing

save space: we just use the original grid to calcuate the min path sum
grid[i][j] represent the min path sum of i x j grid
grid[i][j] = get the min of previous grid(top/left) + current val

Solution:

/**
 * @param {number[][]} grid
 * @return {number}
 */
var minPathSum = function(grid) {
    // save space: we just use the original grid to calcuate the min path sum
    // grid[i][j] = min path sum of i x j grid
    let m = grid.length;
    let n = grid[0].length;
    
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            // grid[0][0] itself contains the min path sum
            if (i === 0 && j === 0) continue;
            // first row: grid[i][j] = previous grid(left) + current val
            if (i === 0) grid[i][j] += grid[i][j - 1];
            // first column: grid[i][j] = previous grid(top) + current val
            else if (j === 0) grid[i][j] += grid[i - 1][j];
            // grid[i][j] = get the min of previous grid(top/left) + current val
            else grid[i][j] += Math.min(grid[i][j - 1], grid[i - 1][j]);
        }
    }
    return grid[m - 1][n - 1];
}