LeetCode 133. Clone Graph (javascript)

Given a reference of a node in a connected undirected graph.

Return a deep copy (clone) of the graph.

Each node in the graph contains a val (int) and a list (List[Node]) of its neighbors.

class Node {
    public int val;
    public List<Node> neighbors;
}

Test case format:

For simplicity sake, each node’s value is the same as the node’s index (1-indexed). For example, the first node with val = 1, the second node with val = 2, and so on. The graph is represented in the test case using an adjacency list.

Adjacency list is a collection of unordered lists used to represent a finite graph. Each list describes the set of neighbors of a node in the graph.

The given node will always be the first node with val = 1. You must return the copy of the given node as a reference to the cloned graph.

Example 1:

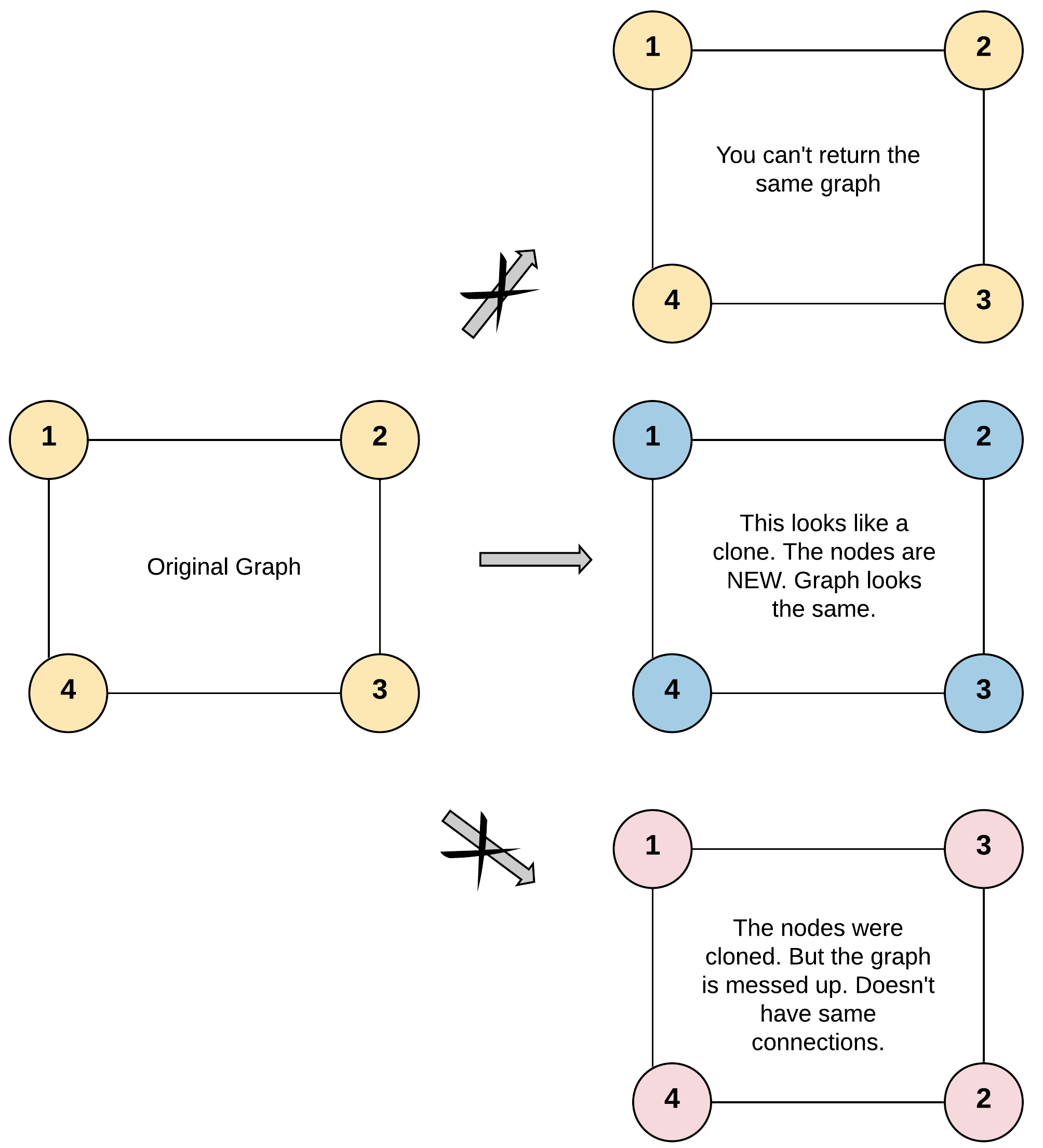
Input: adjList = [[2,4],[1,3],[2,4],[1,3]]
Output: [[2,4],[1,3],[2,4],[1,3]]
Explanation: There are 4 nodes in the graph.
1st node (val = 1)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
2nd node (val = 2)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).
3rd node (val = 3)'s neighbors are 2nd node (val = 2) and 4th node (val = 4).
4th node (val = 4)'s neighbors are 1st node (val = 1) and 3rd node (val = 3).

Example 2:

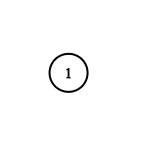
Input: adjList = [[]]
Output: [[]]
Explanation: Note that the input contains one empty list. The graph consists of only one node with val = 1 and it does not have any neighbors.

Example 3:

Input: adjList = []
Output: []
Explanation: This an empty graph, it does not have any nodes.

Example 4:

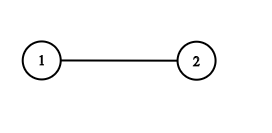
Input: adjList = [[2],[1]]
Output: [[2],[1]]

Constraints:

1 <= Node.val <= 100
Node.val is unique for each node.
Number of Nodes will not exceed 100.
There is no repeated edges and no self-loops in the graph.
The Graph is connected and all nodes can be visited starting from the given node.

Idea:

BFS Queue + HashMap +

我们使用 BFS 来遍历图，使用队列 queue 进行辅助，一个 HashMap 来建立原图结点和克隆结点之间的映射。先克隆当前结点，然后建立映射，并加入 queue 中，进行 while 循环。在循环中，取出队首结点，遍历其所有 neighbor 结点，若不在 HashMap 中，我们根据 neigbor 结点值克隆一个新 neighbor 结点，建立映射，并且排入 queue 中。然后将 neighbor 结点在 HashMap 中的映射结点加入到克隆结点的 neighbors 数组中即可，参见代码如下：

Time complexity: O(V+E) 点+边
Space complexity: O(V+E)

Solution 1:

/**
 * // Definition for a Node.
 * function Node(val, neighbors) {
 *    this.val = val === undefined ? 0 : val;
 *    this.neighbors = neighbors === undefined ? [] : neighbors;
 * };
 */
/**
 * @param {Node} node
 * @return {Node}
 */
var cloneGraph = function(node) {
    if (node === null) return null;
    let map = new Map();
    map.set(node, new Node(node.val));
    let q = []; // queue
    q.push(node);
    while (q.length !== 0) {
        let cur = q.shift();
        for (let n of cur.neighbors) {
            if (!map.has(n)) {
                map.set(n, new Node(n.val));
                q.push(n);
            }
            map.get(cur).neighbors.push(map.get(n));
        }
    }
    return map.get(node);
};

Solution 2:

var cloneGraph = function(node) {
    if (node === null) return null;
    let visited = new Map();
    let map = new Map();
    let q = []; // queue
    q.push(node);
    while (q.length !== 0) {
        let cur = q.shift();
        if (visited.has(cur)) continue;
        visited.set(cur, true);
        if (!map.has(cur)) map.set(cur, new Node(cur.val));
        let temp = map.get(cur);
        for (let n of cur.neighbors) {
            if (!map.has(n)) map.set(n, new Node(n.val));
            q.push(n);
            temp.neighbors.push(map.get(n));
        }
    }
    return map.get(node);
};